本文讲解回溯算法的原理和具体实现。

1 回溯算法

1.1 回溯算法的原理

回溯算法是暴力搜索法中的一种。回溯法是一种可以找出所有（或一部分）解的一般性算法，尤其适用于约束满足问题。
在实际实现时采用DFS搜索的方式进行遍历，然后再遍历过程中采用剪枝的策略去掉不满足条件的解。
对于具体代码实现而言，实际上就是DFS的一种实际应用。和DFS遍历二叉树不同之处在于，回溯中使用DFS需要有前进和回退的过程，这也是为啥叫做回溯的原因。一般在回溯算法中，使用递归的方式来进行DFS。

1.2 解决回溯问题思路

解决回溯问题时，一定要画出遍历路径的多叉树。搞清楚横向遍历的是什么，和纵向遍历的路径是啥？例如：如下图所示，为leetcode 电话号码组合问题中"23"的遍历示意图。其中2对应字符串"abc", 3对应字符串"def"。
我们可以看到，横向展开的是每个字符串内的每个字母，纵向是展开的字符串"23"。
而回溯的递归函数中的for循环内部实现，就是横向展开的体现。
因此在这个问题中，需要先根据索引获取数字对应的字符串。

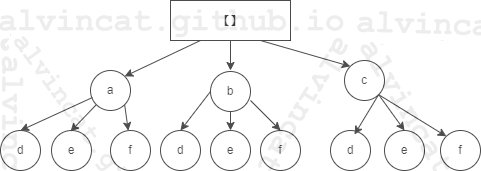
backtrackting_01

而针对问题39-组合总和问题，可以按照下图所示的思路去分析解决：
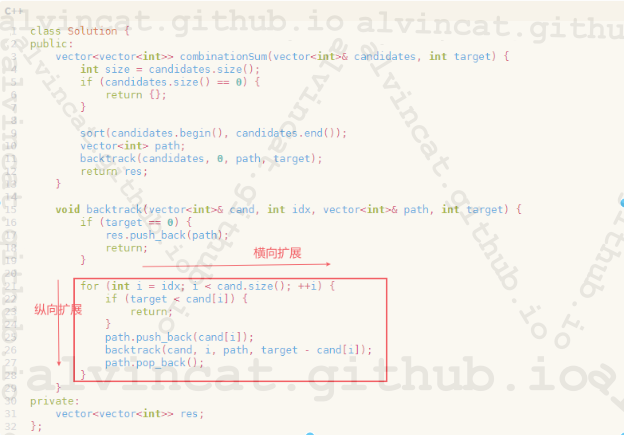
backtrackting_02

1.1.1 回溯代码的基本框架

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


path = []  
def backtrack(path, 选择列表):  
    if 满足结束条件:  
        result.add(item)  
    return  

    for item in 选择列表:  
        path.push(item) // 添加  
        backtrack(path, 选择列表)  
        path.pop()     // 删除

1.2 回溯算法的应用

1.2.1 排列组合问题

问题1: 全排列

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34


class Solution {
public:
 vector<vector<int>> permute(vector<int>& nums) {
     int len = nums.size();
     if (len == 0) {
         return res;
     }

     vector<int> path;
     vector<bool> used(len, false);
     dfs(nums, path, 0, used);
     return res;
 }

 void dfs(vector<int>& nums, vector<int> path, int depth, vector<bool>& used) {
     int len = nums.size();
     if (len == depth) {
         res.push_back(path);
         return;
     }

     for (int i = 0; i < len; ++i) {
         if (!used[i]) {
             path.push_back(nums[i]);
             used[i] = 1;
             dfs(nums, path, depth + 1, used);
             used[i] = 0;
             path.pop_back();
         }
     }
 }
private:
 vector<vector<int>> res;
};

问题2：电话号码的字母组合

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33


class Solution {
public:
vector<string> letterCombinations(string digits) {

    int len = digits.size();
    if (len == 0) {
        return {};
    }

    string path;
    backtrack(digits, 0, path);
    return res;

}

void backtrack(string digits, int index, string& path) {
    if (index == digits.size()) {
        res.push_back(path);
        return;
    }
    char ch = digits[index];
    string str = num_map[ch - '0'];
    for (int i = 0; i < str.size(); ++i) {
        path.push_back(str[i]);
        backtrack(digits, index + 1, path);
        path.pop_back();
    }

}
private:
string num_map[10] = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};
vector<string> res;
};

问题3：组合总和(39)

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32


class Solution {
public:
    vector<vector<int>> combinationSum(vector<int>& candidates, int target) {
        int size = candidates.size();
        if (candidates.size() == 0) {
            return {};
        }

        sort(candidates.begin(), candidates.end());
        vector<int> path;
        backtrack(candidates, 0, path, target);
        return res;
    }

    void backtrack(vector<int>& cand, int idx, vector<int>& path, int target) {
        if (target == 0) {
            res.push_back(path);
            return;
        }

        for (int i = idx; i < cand.size(); ++i) {
            if (target < cand[i]) {
                return;
            }
            path.push_back(cand[i]);
            backtrack(cand, i, path, target - cand[i]);
            path.pop_back();
        }
    }
private:
    vector<vector<int>> res;
};

1.2.2 N皇后问题

1.3 Leetcode相关题目

17 Letter Combinations of a Phone Number
22 Generate Parentheses
39 Combination Sum
46 Permutations
51 N-Queens
52 N-Queens II
77 Combinations
78 Subsets
89 Gray Code
93 Restore IP Addresses
111 Minimum Depth of Binary Tree
112 Path Sum
113 Path Sum II
131 Palindrome Partitioning
140 Word Break II

文章目录